Chapitre 12 - Logarithme Népérien
IGénéralités
Soient \(a\) et \(b\) deux nombres réels (\(a\gt0\) ) tels que \(a = e^b\), alors :
- \(a\) est l'exponentielle de \(b\)
- \(b\) est le logarithme népérien de \(a\)
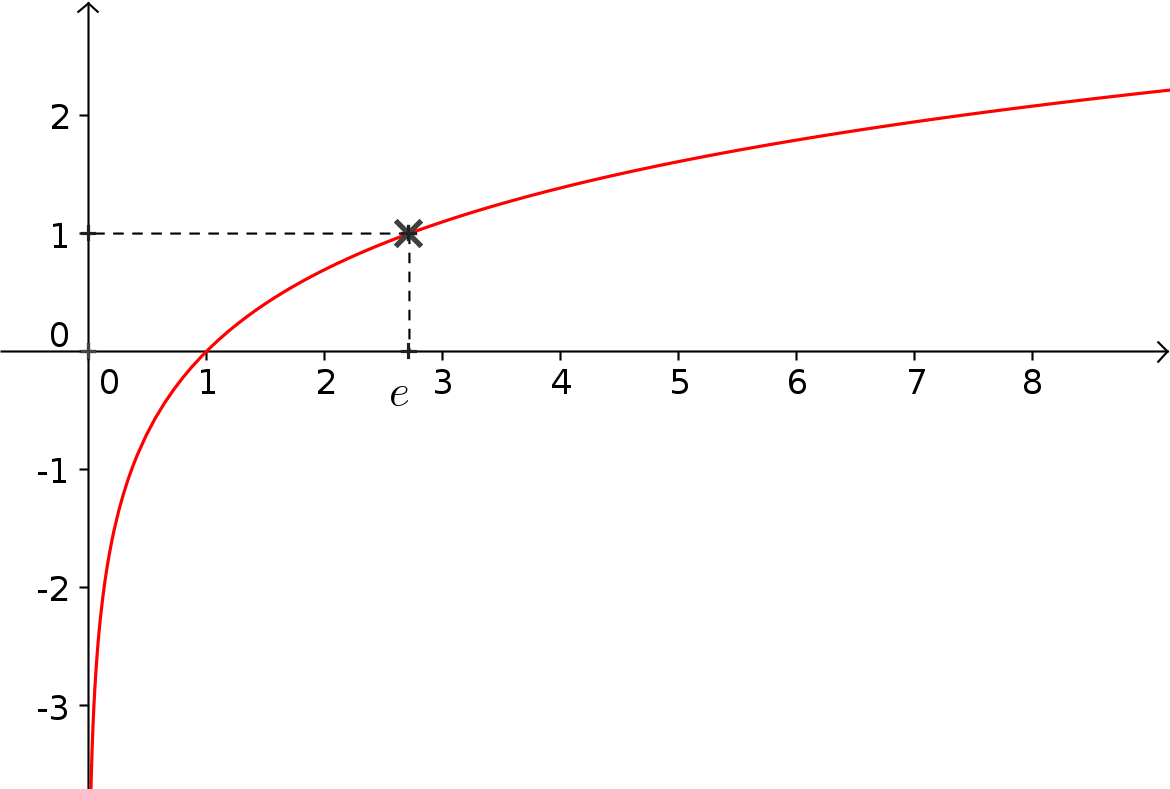
La fonction logarithme népérien d'équation \(f (x) = ln (x)\) est définie sur \(]0;+\infty]\)
En effet, si \(y = ln (x)\), alors \(y\) est l'exponentielle de x : \(x = e^y\) et une exponentielle est toujours positive. Donc \(x \gt 0\).